Density is the mass of a substance divided by its volume. It indicates how much of a substance occupies a specific volume at a defined temperature and pressure. Different materials exhibit different densities. For example, osmium is the densest element known under standard conditions. It is widely used to identify the pure substance and to estimate the composition of different kinds of a mixture; it can be used to define the substance. In chemistry or physics, density is expressed by the symbol ρ or D, and the mathematical expression is p=m/v; that is, density symbol p is equal to the total mass (M) divided by total volume (v). People often get confused between mass and density. Familiar words like ‘heavy’ or ‘light’ refer to mass, not density. A huge sponge may weigh a lot, but its density is low because it weighs a minimal per unit of its volume. Therefore, we consider the size and volume of the object.
Common Units:
Generally, the density of water is taken as the standard value, which is the SI unit of density:
- Kilogram per cubic meter(kg/m3)
The liter and tonne are not part of SI but are used with density. The following other units are:
- Gram per milliliter (g/ml)
- Tonne per cubic metre(t/m3)
- Kilogram per litre(kg/L)
In a qualitative type, it shows the heaviness of an object at a constant volume. Different materials with different masses have different densities for the same volume.
Calculating Density
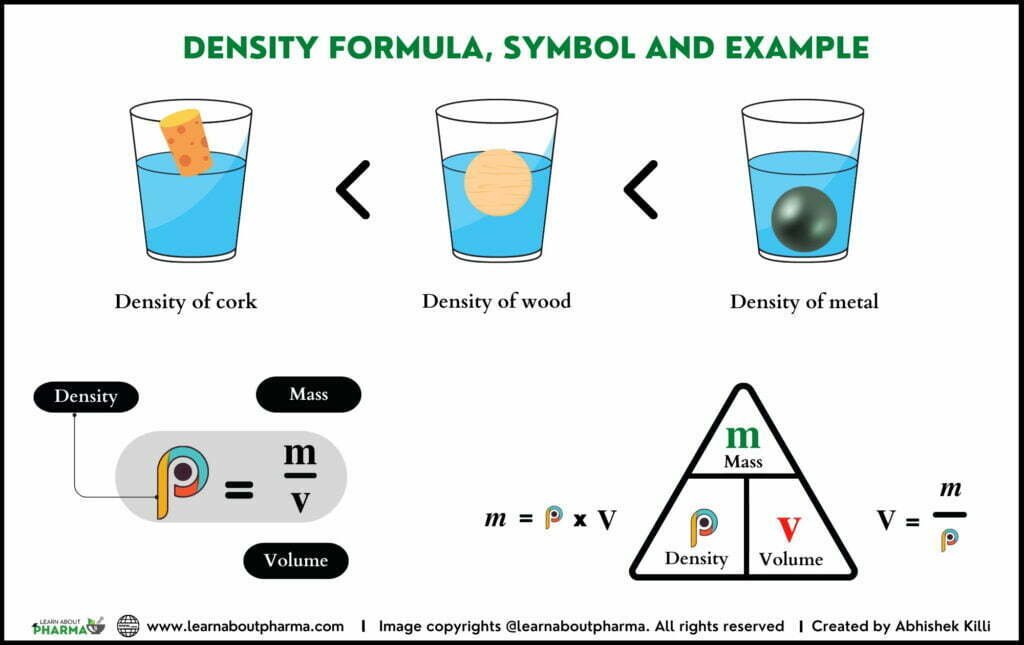
Density cannot be measured directly. If you want to know the density of a material, you will have to weigh it and then measure it with volume. You cannot add densities. The formula used to calculate the density is
D= Mass/Volume.
Question: What is the density of a cube of sugar weighing 11.2grams measuring 2 cm on a side?
Solution:
Density (symbol D)= mass/volume; D= 11.2 grams/8 cm3; D = 1.4 grams/cm3
Densities for gases are on the thousandths of grams per cubic centimeter; liquids have densities of 1.0g/cm^3. Freshwater has about 1.0 g/cm3, rocks around 3g/cm^3, and metals have densities above 6 g/cm^3. The normal density calculators use 0 degrees C and one atmospheric pressure. The ideal gas law formula calculates ideal gases’ molar mass and density. It gives the approximate value under average temperature and pressure. Therefore, Ideal gas equations are not accurate.
The density version of the ideal gas law is PM = dRT, where P is pressure measured in atmospheres (atm), T is temperature measured in kelvin (K), R is the ideal gas law constant 0.0821, but M is now the molar mass (g/mole), and density (g/L) symbol is denoted as d.
By rearranging the formula to PM/RT = d, the units of atm, mol, and K will cancel, and the value will be left with the g/L units for density.
Limiting densities are densities that are calculated from the above gas equation and are only approximate and inaccurate. But are obeyed at very low pressure. It is the density of gas when the ratio of density per unit pressure is extrapolated to zero pressure.
Densities are critical for many uses. One of the many uses of density is to calculate the density of the substance to determine if it will float on another. Even in hot air balloons, the air becomes less dense when heated. The air is heated until the balloon’s total density is less than the atmosphere.
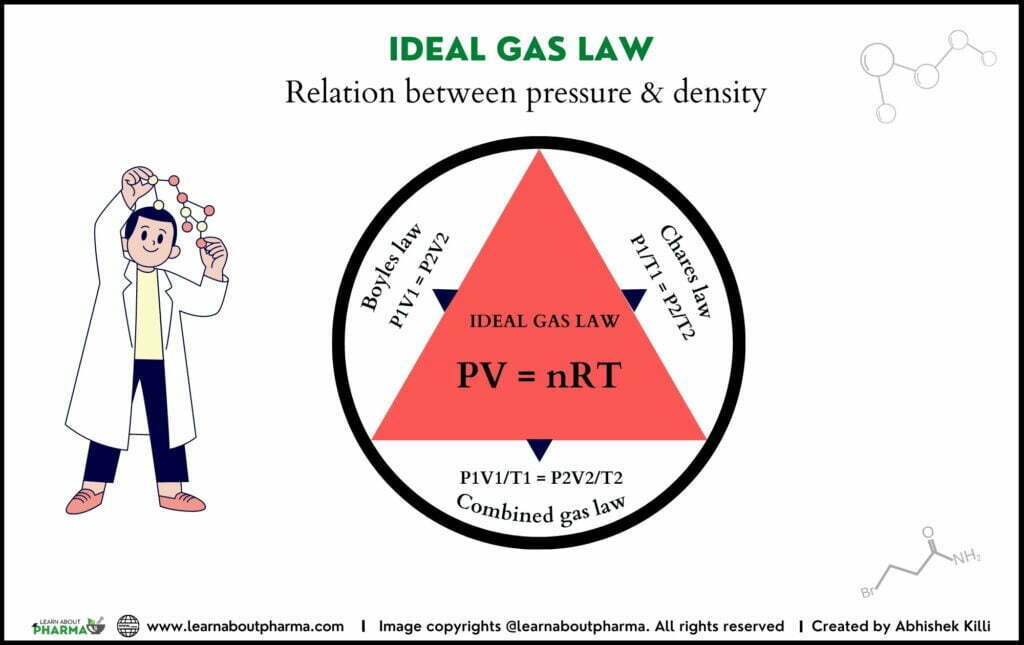
Pressure v/s Density of Ideal gas
The relation between pressure and density is expressed through the equation of states for ideal gases by applying Boyle’s and Charles and Gay-lussac law. By combining both, we get PV = nRT.

Boyle’s law: the volume of a gas at constant temperature varies inversely with the pressure exerted on it
Charles and Gay-lussac’s Law demonstrated that the volume of a gas is directly proportional to its temperature at a constant pressure.
PV /T =nR/T gives: PV = nRT
Dividing both sides with m, we get specific volume, defined as the ratio of volume to its mass.
PV/m=nRT/m (1)
Substituting specific volume in equation (1) which is v= volume(v)/ mass(m)=1/p Pv/M=nRT/M
P=pRT
The pressure and density are directly proportional to each other.
You might also like to read the following curated articles:
Vapour density:
It is defined as the ratio of gaseous substance and hydrogen density under the same temperature and pressure. It may be defined as the mass of a certain volume of a substance divided by the mass of the same volume of hydrogen.
Vapour density (Symbol V.D) = mass of n molecules of gas/mass of n molecules of hydrogen
Abnormal Density:
Certain chemical substances, like ammonium chloride, hydrogen peroxide, etc., have their calculated vapor densities less than the theoretical measurements. Only at a high temp this phenomenon called abnormal densities. This is caused due to thermal bond dissociation.
At the constant pressure because of the dissociation, the volume of the gases increases with the increase of the mole number. The mass remains the same; thus, D* decreases. The total number of moles that suffer dissociation calculates the degree of dissociation.
One molecule of substance A splits up into n molecules of B by specific heat A > nB.
At equilibrium for each g mole of A will be (1 – α) g moles of undissociated A and nα g moles of B. So the total number of g moles of gas present = (1-α) + nα or 1 + (n-1)α. When V = volume occupied per unit volume of gas or vapor and D0 defines the density measurement absence of any dissociation, suppose D denotes the observed density when actual dissociation occurred and the total weight of the gas = W.
W = D0V and W = D×V[1 + (n-1)α]
∴ D0/D = 1 + (n-1)α
At high-temperature a=1, thus density D=Do/2.
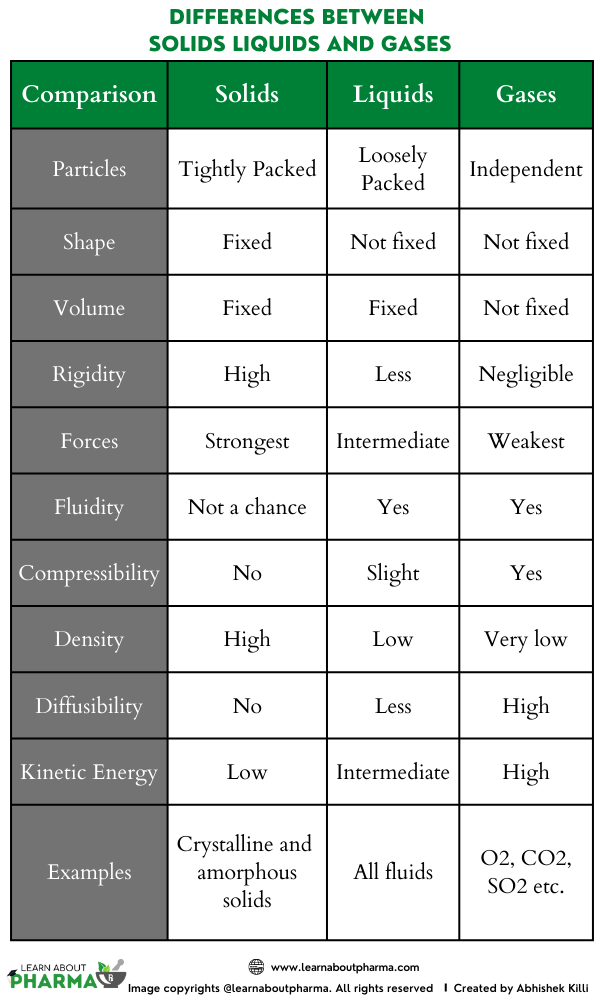
Solids, liquids, and gases
Gasses generally have the lowest densities but are highly dependent on pressure and temperature. They must be specific to the extent to which a gas exhibits ideal behavior. The density of a gas is directly proportional to the masses of its component. Measurement of the density of a gas is equivalent to its molecular weight.
Liquids have an intermediate range of densities. Mercury being a liquid metal, is different in case. They are largely dependent on the pressure but are temperature -sensitive. The density range of solids is quite wide. Metals have tightly packed atoms and have the highest densities, except lithium. The highest metallic is quite low. Composite solids like wood contain void spaces and get reduced to average density.